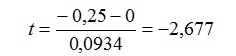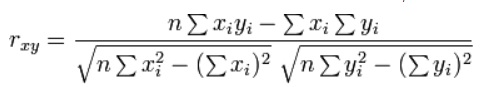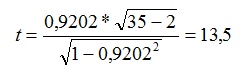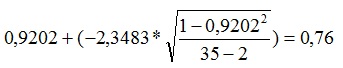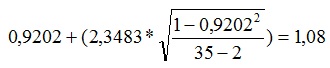RESUMEN
Con este artículo vamos a complementar el artículo de contraste de medias para dos muestras independientes que publicamos con anterioridad. La comparación de medias es una de las pruebas estadísticas más comunes y se emplea con mucha frecuencia en diferentes ámbitos de la investigación. Tal y como hicimos en el caso de dos muestras independientes, vamos a tratar de explicar como nos enfrentaríamos al cálculo e interpretación de esta prueba estadística mediante el uso de una sencilla calculadora (aunque nos hemos servido de Excel para hacer los cálculos y presentar los valores), el uso de la hoja de cálculo Excel y, por supuesto, el programa de análisis estadístico SPSS.
ARTÍCULO: Prueba t de Student para dos muestras relacionadas.
Introducción.
Ya hemos publicado un artículo relacionado con la comparación de la media bajo el supuesto de que las dos muestras son independientes. En este caso, vamos ver cómo realizar la misma comparación de medias, pero en el supuesto de que las dos muestras están relacionadas, es decir, cuando un sujeto es medido en dos condiciones diferentes. Para ello emplearemos el estadístico t para dos muestras relacionadas.
El caso de comparación de muestras relacionadas es muy frecuente cuando, por ejemplo, se está probando la eficacia de un tratamiento. En este caso, tenemos por ejemplo, un grupo de sujetos al que le tomamos una medida antes de la aplicación de un tratamiento (pre-test), seguidamente aplicamos el tratamiento, y volvemos a hacer la misma medida (post-test). Nuestro interés es saber si hay alguna diferencia entre las dos medidas. Si hay diferencias en la media, podemos decir que el tratamiento ha tenido algún efecto y el sentido de las diferencias, mientras que si no hay diferencias, no podemos decir que el tratamiento haya tenido efecto alguno.
Para este caso vamos a usar el siguiente archivo. El problema a resolver seria el siguiente:
Un equipo de psicólogos está poniendo a prueba una técnica de relajación para combatir la ansiedad. Para conocer el grado de ansiedad que presentaban los sujetos se pasó un test de ansiedad a un conjunto de 35 sujetos (mayor puntuación significa mayor ansiedad). Una vez hecho esto, se pusieron en práctica las técnicas de relajación, y seguidamente se volvió a medir el grado de ansiedad que padecían los sujetos. La columna A representa los datos antes del tratamiento, mientras que la columna B representa los datos después del tratamiento. Con estos datos, ¿Qué podemos decir de la eficacia de la técnica de relajación como tratamiento contra la ansiedad?
Supuestos del modelo t de Student para dos muestras relacionadas.
Nivel de medida de las variables: métricas, es decir, de intervalo o razón.
Distribución: normal o aproximadamente normal.
Tipo de diseño: Equilibrado.
Varianza de la diferencia de medias: desconocida.
Observaciones: pre-tratamiento / pos-tratamiento.
Hipótesis que se pone a prueba: la diferencia de medias toma un determinado valor, cero si se asumen iguales.
Bondad de ajuste.
La distribución t de Student es simétrica, al igual que la distribución normal, pero es más aplanada, es decir, su coeficiente de curtosis o apuntamiento es negativo. Cuando el tamaño de la muestra excede de 30 o 35 casos la t de Student se aproxima a la distribución normal. Por tanto es razonable realizar una prueba de Kolmogorov-Smirnov para ver en qué medida se aproxima a la distribución normal. En el caso de rechazo de la hipótesis de normalidad, sería aconsejable la observación del histograma, para observar con mayor claridad el modo en que no se ajusta a la distribución normal. Si, aunque la hipótesis la rechace el estadístico de Kolmogorov-Smirnov, puede observarse algún grado de normalidad (la t de Student será más aplanada que la distribución normal), podemos usarlo, pero teniendo en cuenta este resultado de cara a la interpretación de los datos. En caso de alejarse de manera marcada de la normalidad, sería aconsejable usar una prueba de tendencia central no paramétrica.
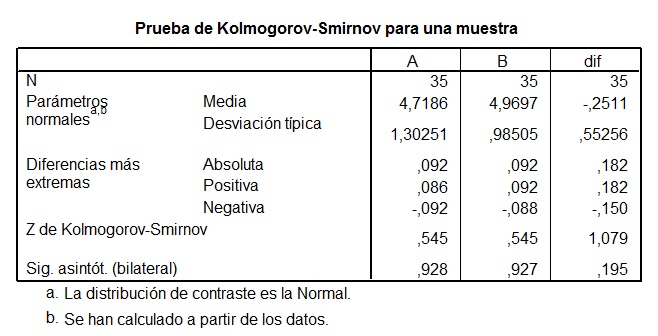
Tabla 1: Prueba del Kolmoorov-Smirnov.
En nuestro caso podemos ver como las muestras “A” (pre-tratamiento), “B” (pos-tratamiento) y “dif” (diferencia entre las muestras A y B) se distribuyen como una normal, dado que la significación del estadístico de Kolmogorov –Smirnov es mayor de 0,05.
Veamos los histogramas
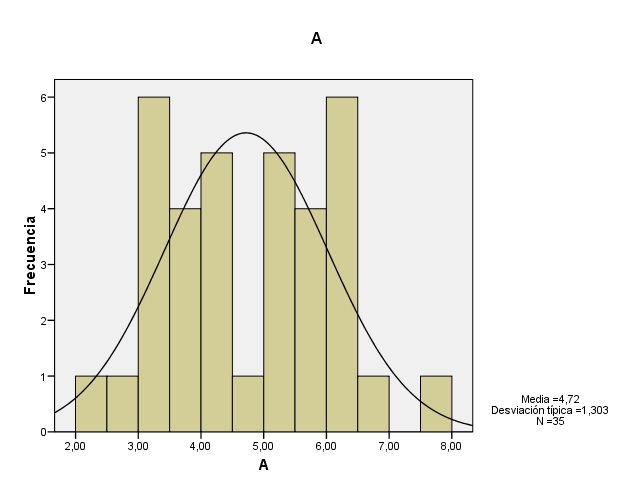
Gráfico 1: Histograma de la muestra A (pre-tratamiento).
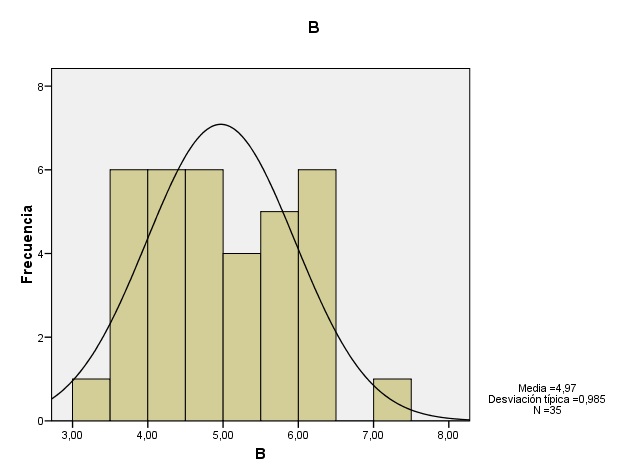
Gráfico 2: Histograma de la muestra B (pos-tratamiento).
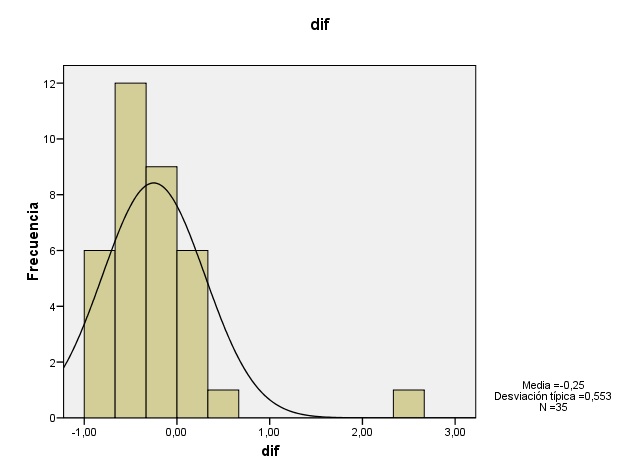
Gráfico 3: Histograma de las diferencias de las muestras (A – B).
Puede observarse como se da cierta simetría en las muestras A y B. En la muestra B puede observarse un claro aplanamiento respecto a la normal, lo que indica curtosis negativa. La gráfica de las diferencias muestra un claro apuntamiento o curtosis positiva, además de un claro desplazamiento de los datos hacia el lado negativo de la gráfica (por debajo de la media) que indica una alta asimetría positiva.
Aún estas particularidades, puede observarse que las tres distribuciones se asemejan a la distribución normal. En este caso, dado que Kolmogorov-Smirnov nos indicaba que era razonable asumir la normalidad, no era necesario analizar las gráficas. Pero se ha hecho con intenciones didácticas y analíticas
Hipótesis y estadístico de contraste.
Tabla 2: Resumen del modelo de inferencia t de Student para dos muestras relacionadas.
La hipótesis nula se establece sobre el valor que toma la diferencia de medias. Si la diferencia de medias se establece en cero, significa que estamos asumiendo que las medias en las dos muestras (pre y pos tratamiento) serán iguales, por tanto el tratamiento no ha tenido efecto. Por supuesto, también podemos establecer que la diferencia entre las dos muestras tiene que ser superior a un valor para considerar que el tratamiento ha sido efectivo. En este caso debemos tener en cuenta la diferencia que asumimos, e interpretar los resultados en función de ese supuesto. Si asumimos que la diferencia debe ser de un punto entre el pre-tratamiento y el pos-tratamiento para que el tratamiento pueda ser considerado como efectivo, y aceptamos la hipótesis nula, estamos diciendo que el tratamiento ha sido efectivo.
Error a priori y regiones críticas.
En todo proceso inferencial consideraremos antes de los análisis el error que estamos dispuestos a cometer. En términos generales es común usar un alpha de 0,05. Es preciso también tener en cuenta la direccionalidad del contraste, asumiremos un contraste bilateral o de dos colas, es decir, asumimos que puede haber diferencias, pero no especificamos si se situaran por el encima o por debajo de los valores asignados a la hipótesis nula.
En nuestro caso asumiremos que la hipótesis nula establece que las medias de las dos muestras son iguales, es decir, su diferencia será cero.
Por tanto, la región de aceptación donde se encontrará el estadístico de contraste según el modelo t de Student para un contraste bilateral con una probabilidad alpha de 0,05 / 2 = 0,025 y un número de pares de casos (pre y pos-tratamiento) de 35 – 1 = 34 grados de libertad. Mediante la tabla de la t de Student podemos determinar la región de aceptación buscando en lugar no 0,025 sino 0,975 (1 – 0,025 = 0,975), dado que la tabla ofrece solo una mitad (la positiva) de la distribución, y dado que esta es simétrica, para obtener el limite inferior solo tendremos que multiplicar por -1. Por tanto, dado que no existe en esta tabla el valor 35, nos quedamos con la última fila (aproximación al infinito) y vemos que la puntuación asociada a 0,975 es 1,96. Por tanto la región de aceptación de la hipótesis nula está comprendida entre los valores críticos mayores que -1,96 y menores que 1,96. La función de Excel DISTR.T.INV(ALPHA;GRADOS LIBERTAD) nos dará este valor con toda precisión, que es 2,032244498. La función de Excel nos da por tanto un intervalo comprendido entre las puntuaciones -
2,032244498 y 2,032244498. La diferencia con el valor de las tablas viene dada por que la tabla, en este caso, da una aproximación. Siempre que sea posible use Excel u otro programa para obtener los valores críticos, evitando el uso de tablas salvo que no tenga otra opción.
Cálculo del estadístico.
Aunque lo laborioso, no complejo, de este cálculo hace aconsejable el uso de programas de análisis estadístico (después se mostrará ésto), veremos qué cálculos tenemos que hacer para llegar a obtener el estadístico t para dos muestras relacionadas (también conocido como estadístico t para dos muestras emparejadas).
Si queremos ver el detalle del cálculo de cómo se haría de manera manual, utilizaremos Excel para realizar las operaciones, abra este documento. Si no tiene conocimientos de Excel, consulte nuestro curso
intensivo de Excel.
Necesitamos calcular los siguientes valores:
1) La media de las diferencias de medias.- puede verla en la celda D40, y toma el valor -0,25114286.
2) Desviación típica de la diferencia menos la diferencia de medias.- puede verla en la celda E40, y toma el valor 0,552559666.
3) Error típico de la diferencia de medias.- puede verlo en la celda E42 y toma el valor 0,093399631. Se ha obtenido mediante la formula 0,552559666 / 5,916 que es la raíz cuadrada del tamaño muestral 35.
4) No olvidemos que hemos considerado que la diferencia entre las medias será 0. Es decir, la hipótesis nula que ponemos a prueba es que las medias son iguales.
Así, el estadístico t tomará el siguiente valor:
Formula 1:
Con los valores que calculamos con Excel, hemos calculado el estadístico t mediante una calculadora. El valor que hemos obtenido ha sido aproximadamente el mismo -2,677. Esta variación se produce por la pérdida de decimales, lo que es muy frecuente en estadística cuando se usa una calculadora para realizar los cálculos.
El cálculo de los valores realizados en la hoja de cálculo pueden verse interpretando las fórmulas que puede ver en las celdas donde aparecen. Si no tiene conocimientos de Excel, visite nuestro curso de Excel.
Por tanto, dado que el valor -2,677 es menor que el valor critico que nos daba la tabla de la t de Student -1,96 ó que -2,03 que nos daba Excel, podemos decir que la diferencia entre las medias es distinta de cero, y por tanto las medias de las muestras A y B son significativamente diferentes. Es decir, nuestro estadístico que encuentra en la región de rechazo de la hipótesis nula, la región critica. Recuerde que la región que acepta la hipótesis nula, se llama región de aceptación de la hipótesis nula. Esto nos conduce a afirmar que el tratamiento ha tenido efectos.
También podemos hacer la inferencia en función de la probabilidad del estadístico de contraste (valor p), es decir, de la probabilidad del estadístico t. Dado que la tabla de la que disponemos sólo ofrece los valores de la mitad positiva, y puesto que esta distribución es simétrica, buscaremos el estadístico pero con signo positivo. Si no lo encontramos, tomamos el más próximo. De esta manera buscamos el valor obtenido con Excel, dado que es más preciso, vemos que encontramos 2,68 en la columna de la probabilidad 0,99. Así, la probabilidad de obtener un estadístico con valor menor o igual a 2,68 es 0,99 (ya que está en la columna del 0,99). Por tanto la probabilidad de obtener un estadístico mayor o igual que 2,68 es 0,01. En el caso de tratarse del estadístico negativo, la interpretación es similar. La probabilidad de obtener un estadístico menor o igual de -2,68 es 0,01, por tanto la probabilidad de obtener una estadístico mayor o igual es 0,99. Así, dado que decidimos usar un alpha de 0,05, y 0,01 es menor que 0,05, no podemos afirmar que la diferencia de las medias sea igual a cero, esto es, las medias son diferentes. A este resultado ya habíamos llegado cuando posicionamos el estadístico de contraste fuera de la región de aceptación de la hipótesis nula, es decir, en la región critica.
Cálculo con Excel.
Excel tiene una función llamada “Prueba t para dos muestras emparejadas” en el menú Herramientas – Análisis de datos (tenga en cuenta que esta opción de análisis no se instala de manera predeterminada en la típica instalación de Excel, consulte nuestro curso de Excel). Con esta función solamente tenemos que determinar el nivel alpha, la diferencia hipotetizada para las medias y nos dará una tabla como la siguiente:
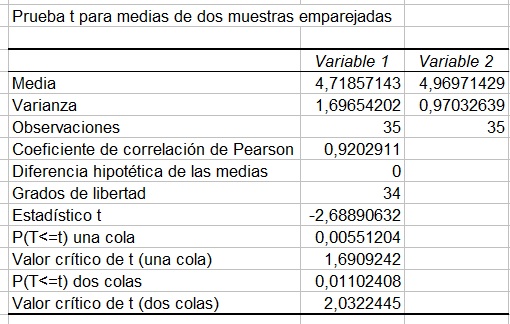
Tabla 3: Resultados de Excel para t de Student con dos muestras emparejadas.
Esta tabla nos ofrece algunos estadísticos descriptivos como media, varianza, número de casos, grados de libertad, etc. el valor del estadístico t.
En esta tabla vemos el valor del estadístico t que es -2,6889. El punto positivo que delimita la región critica y de aceptación para el caso bilateral aparece como valor critico para dos colas 2,0322 (el negativo seria -2,0322 recuerde que la distribución es simétrica). También aparece el valor crítico para una cola, es decir, cuando en la hipótesis nula asumimos un sentido a las diferencias y planteamos la hipótesis nula como: la media de A es mayor que la media de B. Podemos ver que el valor positivo para una cola es 1,69, el valor negativo seria por tanto -1,69. En este sentido, si nuestra hipótesis hubiera sido que la media de la muestra A es menor que la media de la muestra B, dado que nuestro estadístico toma el valor -2,6889, y este es menor que -1,69 si habríamos aceptado que la media de A es menor que la media de B.
La tabla también nos ofrece la probabilidad del estadístico t (valor p) en el caso de contraste bilateral y vale 0,011. En el caso unilateral la probabilidad del estadístico vale 0,0055. Cuando la hipótesis es bilateral, si este valor es menor o igual que alpha / 2 rechazamos la hipótesis nula. En el caso del contraste unilateral rechazamos la hipótesis nula si la probabilidad del estadístico (valor p) es menor o igual que alpha.
Análisis de la relación entre las variables.
Hasta aquí hemos analizado la diferencia de las medias, pero no hemos analizado la relación entre ellas. La relación entre dos variables de tipo metrico viene expresada en el valor del coeficiente de correlación de Pearson. Este valor viene expresado por la formula:
Tabla 4: Coeficiente de correlación de Pearson.
La correlación de Pearson es uno de los coeficientes de relación estadística más usados en todas las disciplinas científicas. Este coeficiente indica el grado de relación existente entre dos variables. Una correlación perfecta positiva tomará el valor 1 e indicará que a medida que los valores de una variable aumentan, también aumentan los de la otra en la misma proporción. Cuando la correlación es negativa y perfecta tomará el valor -1 e indicara que a medida que los valores de una variable aumentan, los de la otra disminuyen en la misma proporción. Cuando la correlación toma el valor 0 indica que no existe absolutamente ninguna relación entre las variables. Lógicamente, como el lector puede imaginar, es muy raro encontrar correlaciones perfectas, ya sean positivas, negativas o nulas.
Aunque el lector que vea por primera vez la formula de la correlación de Pearson pueda verla muy compleja, no lo es tanto, aunque su cálculo es laborioso. Por ello vamos a usar la función de Excel que nos realiza rápida y cómodamente este laborioso cálculo, es la siguiente: COEF.DE.CORREL(RANGO A;RANGO B).
En la celda D46 podemos ver que la correlación de Pearson toma el valor 0,92, lo que es un valor muy alto. Quiere decir pues que las dos variables están muy relacionadas y que la relación es positiva, es decir, los aumentos en una variable conducen a aumentos en la otra variable. El cuadrado de el coeficiente de correlación se denomina coeficiente de determinación que viene a explicar la proporción de variación que una variable puede pronosticas o predecir de la otra. En este caso la determinación vale 0,8464 o lo que es lo mismo, cada variable puede predecir la otra en un 84,64%. Lo que es un valor considerablemente alto.
Ahora nos quedaría determinar si es posible que la relación entre estas variables se deban al azar, para ello vamos a someter a prueba si la correlación de Pearson obtenida es significativa.
Para ello emplearemos el estadístico t de Student (hay muchos estadísticos t, no solo uno) que establece como hipótesis nula que la correlación vale 0, es decir que no hay relación. Por tanto, necesitamos rechazar la hipótesis nula para poder afirmar que hay relación entre las variables que estamos analizando.
En cuanto a los supuestos para este modelo de inferencia, son los siguientes:
Hipótesis nula: establece que la correlación es igual a cero, es decir, que no hay relación entre las variables.
Distribución normal bivariante: es decir, las dos variables tomadas en conjunto deben distribuirse aproximadamente como una normal. Esto se cumple siempre que las dos variables de manera independiente se distribuyen como una normal.
Nivel de medida de las variables: métricas, es decir, intervalo o razón.
El estadístico es el siguiente:
Tabla 5: Estadístico t para el coeficiente de correlación de Pearson.
Formula 2:
Siguiendo la misma lógica que ya cometamos para la determinación de la región de aceptación para el estadístico media, lo hacemos ahora para un contraste bilateral con alpha 0,05 y con 35 – 2 = 33 grados de libertad. La región de aceptación esta determinada por los valores comprendidos entre -2,034515287 y 2,034515287 (muy parecidos a los que teníamos para el contraste de las medias, pero entonces era con 34 grados de libertad). Como vemos el estadístico 13,5 queda muy lejos de estar dentro de la región de aceptación de la hipótesis nula, por lo que rechazamos la hipótesis nula que establecía que la correlación era igual a cero. Por tanto podemos decir que hay una relación lineal significativa entre las variables, y que esta relación es muy alta ( está muy próxima a 1).
De igual manera llegamos a la misma conclusión cuando calculamos el valor p del estadístico, este toma un valor de aproximadamente 0 (el valor del estadístico más alto que ofrece la tabla de la t de Student es 3,29 y la probabilidad de una mayor es 0,0005), por tanto, y de igual manera rechazamos la hipótesis de que la correlación sea igual a 0, y asumimos una relación lineal entre las variables.
También podemos calcular el intervalo de confianza para determinar que rango de valores puede tomar el coeficiente de correlación. Usando las formulas del intervalo de confianza de la tabla 5 tenemos:
Necesitamos conocer los valores críticos para alpha igual a 0,05 y el caso de un contraste bilateral con 35 – 2 = 33 grados de libertad. Para 0,025 es -2,3483 y para 0,975 es 2,3483
El límite inferior será:
Formula 3:
El límite superior será:
Formula 4:
Puede descargar la hoja de cálculo del estadístico t para la correlación y el intervalo de confianza desde aquí.
Podemos ver como el valor mínimo de correlación en nuestro caso será de 0,76. Esto quiere decir que las correlaciones menores no serán significativamente diferentes del cero, es decir, no habría relaciones entre las variables.
De la misma manera podemos ver que el límite superior del intervalo para la correlación supera su máximo valor posible, que como sabemos es de 1. Esto no quiere decir que pueda existir una correlación superior a 1, sino que el rango para la aceptación de una correlación significativa es más amplio bajo el coeficiente de correlación hallado, que por encima de este. Más concretamente, dado que 0,9202 – 0,76 = 0,1602 siendo este el error de estimación, aceptaremos correlaciones que varíen por debajo de la obtenida 0,16 puntos, mientras que por encima solo podremos aceptar correlaciones que superen nuestro valor en 0,0798. Lo que nos viene a decir, que es más probable obtener correlaciones por debajo de la obtenida, que por encima de ella.
Cálculo con SPSS.
El método de realización de un análisis para comparar dos muestras relacionadas con SPSS es muy sencillo.
En el menú Analizar – Comparar medias – Prueba t para dos muestras relacionadas.
El resultado es el siguiente:
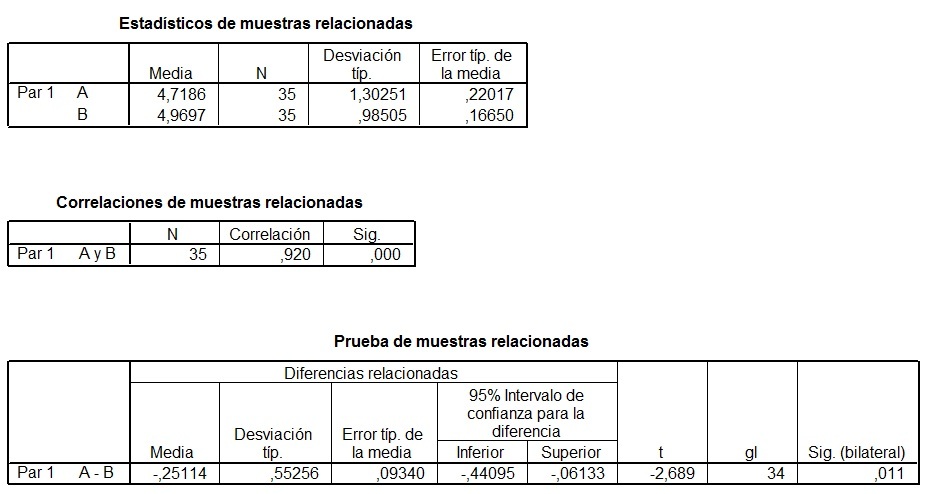
Tabla 6: Comparación mediante la t de Student de dos muestras relacionadas con SPSS
La primera de las tres tablas nos da los estadísticos descriptivos más comúnmente usados.
La segunda nos da la correlación y la significación de la prueba t, como ya dijimos, si el valor p o significación estadística es menor que alpha, aceptamos que la correlación es significativamente diferente de 0, es decir, existe relación entre variables.
La tercera y última tabla nos da la prueba t con un alpha de 0,05 (nos ofrece el nivel de significación 1 – 0,05 = 0,95 = 95%) y vemos como la diferencia entre las medias es de -0,25114 y que el límite aceptable esta comprendido entre los valores -0,44 y -0,06. Como vemos, la diferencia se encuentra dentro de ese intervalo, por tanto asumimos que las medias son diferentes. También podemos ver el estadístico t que vale -2,689 y junto a el su significación o valor p que vale 0,011. Dado que este valor es menor que 0,025 (0,05 / 2 = 0,025 dado que el contraste es bilareral) rechazamos la hipótesis nula de igualdad de medias.
Conclusión final.
En vista de los datos obtenidos podemos ver como los diferentes métodos inferenciales y formas de calcularlo, manualmente, con Excel y con SPSS han ofrecido los mismos resultados. Hemos visto como la forma de ofrecer los resultados no es idéntica, pero también hemos visto que salvo pequeños detalles, la información es la misma aunque expresada de forma diferente.
La cuestión que habíamos planteado en un principio nos pedía una valoración del resultado de la técnica de relajación con respecto al nivel de ansiedad. Los resultados que podemos extraer de los datos son los siguientes.
Dado que la muestra pos-tratamiento (muestra B) tiene una media de ansiedad mayor que la muestra pre-tratamiento (muestra A) podemos decir que el tratamiento contra la ansiedad en vez de reducirla la aumenta. Dada la significación de la prueba, podemos afirmar que este aumento no parece que sea debido al azar. Por otro lado, la correlación tan elevada y significativamente diferente de cero nos dice que efectivamente la relación no puede ser explicada por valores extremos en una o en otra variable que puedan de alguna manera afectar únicamente a las medias. Las diferencias entre una y otra muestra están diseminadas a lo largo de la mayoría de los valores de cada una de las variables. La capacidad explicativa de una variable respecto a la otra es de 0,92022 = 0,8468 o lo que es lo mismo el 84,68 % de cada una de las variables puede ser predicho por la otra.
En vista de los resultados contradictorios, sería conveniente analizar las condiciones en las que se ha aplicado la técnica de relajación, la validez de la técnica, o la adecuación de dicha técnica de relajación a los sujetos tratados.
REFERENCIAS
COMENTARIOS
Publica tu comentario sobre este artículo
Muy ilustrativo
Publicado por Mary. Fecha: 26-05-2022 12:01.
Muchas gracias por la clase. Cuando lo saques en video por YouTube, ganarás el Nobel.
Muy util
Publicado por Pablo. Fecha: 07-04-2018 19:32.
Gracias por el artículo, muy bien explicado. Solo tengo una pregunta: ¿De donde o de que libro son las fórmulas?, en particular el usado para el intervalo de confianza para el coeficiente de correlación. De antemano, Gracias!!
SOBRE LA PUBLICACIÓN
¿El artículo ha sido revisado? NO
Sobre el autor
- Nombre de usuario: ant123
- Formación: Máster en metodología de las ciencias del comporta
- Enviar mensaje al autor
- Fecha de publicación: 17-11-2011 19:36
- Actualice este artículo (Solo puede hacerlo su autor).
- Fecha de actualizacion: 16-05-2012 11:19