Conexionismo
Publica tus artículos en conexionismo.com
Tweet
Con el análisis de varianza entramos en las técnicas multivariantes, es decir, las técnicas que se encargan de analizar más de dos muestras. La lógica inferencial que siguen estas técnicas es idéntica a los modelos ya vistos para la comparación de dos muestras, y por tanto las mismas descritas en términos generales.
Como ya se dijo con otras técnicas, como la prueba t, el cálculo es deseable que se realice mediante un programa de análisis estadístico dado que los cálculos, si no complejos, si resultan muy laboriosos. Esto se hace una realidad evidente con el análisis de varianza que vamos a ver en este artículo. Por tanto, aunque ofreceremos todo el cálculo necesario para que sea posible realizarlo mediante una calculadora, ya va siendo momento de empezar a familiarizarse, al menos con Excel, aunque también veremos como desarrollar estos cálculos con SPSS.
El análisis de varianza de un factor o ANOVA para tres o más muestras independientes, viene a ser una extensión de la prueba t de Student para dos muestras independientes.
La lógica del análisis de varianza de un factor es someter a análisis la variabilidad encontrada en cada uno de los factores, y en función de ella, dar una respuesta sobre el supuesto de igualdad de sus medias.
Aunque seria posible buscar una respuesta estadística usando la prueba t para dos muestras con cada una de las muestras de interés, el error tipo I seria más alto que con el análisis de varianza, de aquí que sea este preferible. Esta afirmación es extensible a otras pruebas. El uso de pruebas bivariadas (para dos muestras) para el caso de tres o más muestras solo nos proporcionará una aproximación al problema, y solo lo haremos en el supuesto de imposibilidad de usar la prueba pertinente, y la decisión estará supeditada a un alpha de al menos el doble de valor que el usado en la prueba multivariada.
ARTÍCULO: Análisis de varianza de un factor para muestras independientes.
Introducción al análisis de varianza.
La situación que trata de resolver el ANOVA de un factor es similar a la que se resolvía mediante la prueba t de Student para dos muestras independientes.
El estadístico t de Student trata de dar una respuesta ante el supuesto de igualdad de dos muestras. No obstante, esta condición en la mayoría de los casos puede ser demasiado simplista. Imaginemos un caso común:
Mediante la prueba t de Student llegamos a la conclusión de que la técnica X de relajación es efectiva para el tratamiento de la ansiedad.
Pero ahora nos podemos plantear si es igual de efectiva para los hombres y para las mujeres, o nos podemos preguntar por la duración óptima de la aplicación de la técnica de relajación. El diseño se va haciendo cada vez más complejo, pero también nos da más respuestas sobre nuestro objeto de estudio. De esta manera el caso de estudio, como ejemplo, podría ser el siguiente:
Mediante la prueba t de Student llegamos a la conclusión de que los sujetos que practicaban la técnica de relajación X puntuaban más bajo en ansiedad que lo que no la practicaron.
Vista su efectividad, vamos a tratar de afinar los resultados determinando si el tiempo de ejecución de la técnica influye en su efectividad, las dos condiciones son: tiempo A (15 minutos al día 5 días a la semana), y tiempo B (30 minutos 3 días a la semana). Pero no nos quedaremos aquí, también analizaremos los datos en función de si el tiempo se les aplica a los hombres y a las mujeres. (Este será nuestro problema de referencia)
Como vemos, las repuestas que buscamos nos las podría ofrecer también la prueba t de Student para dos muestras independientes, si cada condición la vamos comparando con las demás. Pero por este método nos aumentaría la probabilidad de cometer error tipo I, es decir, aumentaría la probabilidad de que rechazásemos la hipótesis nula cuando es cierta. No entraremos en la demostración matemática que lo justifica, pero debemos saber por que debemos usar el análisis de varianza en lugar de múltiples pruebas t.
Una vez situados en el contexto del problema, vamos a proceder a analizar en que consiste el análisis de varianza.
Como ya se ha dicho, el análisis de varianza somete a comparación las medias de tres o más muestras independientes, pero lo hace a partir de la variabilidad (o dispersión de los datos) encontrada en ellas. De esta manera, hay que diferenciar dos fuentes de variabilidad, la que variabilidad debida al factor estudiado (en nuestro caso el nivel de ansiedad), y la variabilidad debida al error experimental (no olvidemos que todos nuestros experimentos se verán afectados en menor o mayor medida por variables extrañas).
En el análisis de varianza de un factor debemos diferenciar entre:
Variable independiente o factor: se refiere a cada una de las categorías en que se mide la variable dependiente, por ejemplo, según el tiempo de duración de la técnica de relajación o en función del sexo, o una combinación de ambas. Estas categorías pueden ser de tipo nominal u ordinal.
Variable dependiente: es la variable que queremos saber si experimenta cambios en función de cada condición factorial, en nuestro caso la ansiedad. Esta variable será de tipo métrico, es decir, de intervalo o razón.
Si hay cambios con respecto a su media, podemos saber en que categoría o factor se produce, lo que nos permitirá llegar a una serie de conclusiones. Esta variación, en nuestro caso, podría ser consecuencia de factor que hace diferentes al los grupos, la técnica de relajación aplicada, el sexo, o una combinación de ambas. En este sentido es preciso tener en cuenta que no todas las comparaciones necesariamente van a ser de interés para nosotros. Tengamos en cuenta que en un análisis con 7 factores el número de comparaciones posibles será de:
Formula 1: Número de comparaciones entre factores.
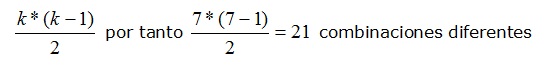
Supuestos del modelo ANOVA de un factor.
Nivel de medida de las variables independientes: la variable independiente es una categorización de las condiciones de medida de la variable dependiente, por tanto, lo que en si la convierte en variable no métrica (nominal u ordinal), es la definición de las variables o factores, no los valores que toman cada una de estas categorías. En nuestro caso, las medidas de ansiedad en cuanto a sexo, o en cuanto a tiempo, es lo que constituye el nivel de medida nominal u ordinal, no los propios valores que toman cada una de los sujetos. Será por tanto la pertenencia a un grupo, categoría o factor, el responsable de las diferencias en las medias de la variable dependiente, en nuestro caso, la ansiedad.
Nivel de medida de la variable dependiente: será de tipo métrico (intervalo o razón).
Tipo de distribución: normal o aproximadamente normal.
Tipo de diseño: equilibrado o no equilibrado.
Observaciones: aleatorias e independientes.
Criterio fundamental a considerar: homogeneidad de varianzas.
Bondad de ajuste.
La prueba de normalidad de distribución de cada factor (o variable independiente) puede hacerse mediante el estadístico Chi cuadrado de Pearson cuando lo aplicamos a datos agrupados, o mediante la prueba de Kolmogorov-Smirnov.
El tipo de diseño, equilibrado o no equilibrado tendrá repercusión en el método de cálculo que identifica las medias responsables del rechazo de la hipótesis nula. En el caso de modelos equilibrados tenemos en consideración el tamaño del grupo o factor, en el caso de modelos no equilibrados, tomaremos en consideración la media armónica del tamaño de los diferentes grupos.
La independencia de las observaciones puede ser probada mediante el estadístico t de Student para la correlación de Pearson. Dicho estadístico se vio en el artículo de comparación de dos muestras relacionadas mediante la prueba t de Student. Esta prueba habría que ponerla a prueba en comparaciones dos a dos, por lo que seria preferible usar una prueba como el test de Rachas.
La homogeneidad de varianzas puede analizarse mediante el test de Cochran cuando nuestro modelo es equilibrado, o el test de Bartlett si el modelo no es equilibrado. SPSS analiza la homogeneidad de varianzas con el estadístico de Levene.
Definición de las variables.
Sobre el planteamiento hecho en nuestro problema de referencia, vamos ahora de definir las variables que analizaremos en nuestro modelo.
En este caso partimos de un conjunto de sujetos de ambos sexos y los asignamos de manera aleatoria a las siguientes categorías:
Variable A: ambos sexos sin terapia de relajación.
Variable B: ambos sexos con la terapia tiempo A.
Variable C: ambos sexos con la terapia tiempo B.
Variable D: mujeres con terapia tiempo A.
Variable E: mujeres con terapia tiempo B.
Variable F: hombres con terapia tiempo A.
Variable G: hombres con terapia tiempo B.
Con este diseño podremos comprobar como se comporta nuestra terapia de relajación para el tratamiento de la ansiedad, según sea el sexo y los tiempos de aplicación. Mientras más efectiva sea la terapia de relajación, los valores de ansiedad serán más bajos.
Para ilustrar nuestro análisis vamos a tomar en consideración los datos del siguiente archivo de referencia, que consta de tres hojas, su contenido es el siguiente:
Hoja Datos.- contiene los valores de puntuación en ansiedad en cada una de las condiciones (o factores) descritos con anterioridad.
Hoja Excel.- contiene el análisis de datos realizando los cálculos con Excel, y la tabla resultado del análisis mediante la función de análisis de datos de Excel.
Hoja SPSS.- Contiene los datos agrupados para su análisis con SPSS.
Estadístico ANOVA de un factor para muestras independientes.
El ANOVA de un factor pone a prueba la hipótesis nula que afirma que todas las muestras tienen la misma media.
Dado que el ANOVA analiza la variabilidad de los diferentes factores, distinguiremos entre variabilidad entre los diferentes niveles (MCinter) y variabilidad dentro de cada nivel (MCintra). De esta manera, lo primero será calcular cada una de estas medias cuadráticas, donde la media cuadrática inter nivel (entre niveles) es un estimador sesgado de la varianza poblacional, y la media cuadrática intra nivel (dentro de cada nivel) será un estimador insesgado de la varianza poblacional.
Siguiendo este razonamiento, el estadístico ANOVA se distribuye como una F de Snedecor, dado que las medias cuadráticas se distribuyen como una Chi de Pearson.
Tabla 1: modelo ANOVA de un factor.

Donde I es el número de factores, y N es el número de sujetos.
Cálculo del ANOVA de un factor con Excel.
Los cálculos a realizar para llevar a cabo el estadístico ANOVA para más de dos muestras independientes pueden verse realizados en la hoja de cálculo Excel del documento de referencia.
Las formulas y datos con que se opera pueden ser extraídas de la hoja de cálculo Excel. Si no conoce el funcionamiento de este programa, le remito a nuestro curso básico de Excel.
El resultado de aplicar los cálculos a nuestro conjunto de datos es el siguiente:
Tabla 2: Cálculo del ANOVA de un factor con Excel.
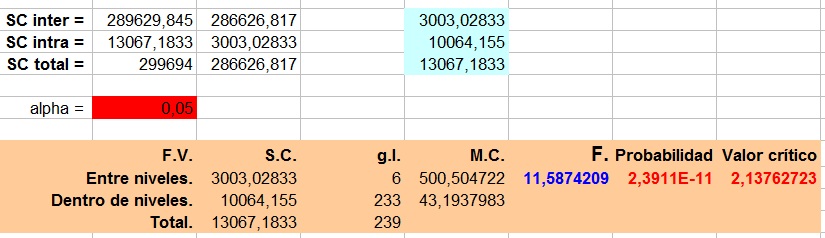
Puede verse como esta tabla contiene los mismos valores que aparecen en la hoja Excel entre las celdas J2 y P20. La diferencia entre un cálculo y el otro es que este ultimo se ha realizado con la función de Excel de análisis de datos, mientras que la imagen 1, refleja los mismos valores pero calculados introduciendo cada una de las formulas de manera manual en Excel.
Como podemos ver el estadístico F toma el valor 11,59 (aproximadamente) dado que su probabilidad es aproximadamente 0 (2,3911E-11), podemos concluir que al menos un factor difiere en su media con respecto a los demás.
Por otro lado, respecto al valor crítico 2,14 (aproximadamente), vemos que el estadístico F toma un valor mayor 11,59 (aproximadamente), lo que nos lleva ha hacer la misma afirmación que ya hicimos antes, es decir, al menos un factor difiere en su media con respecto a los demás.
Modelo de efectos aleatorios frente a modelo de efectos fijos.
Como ya se comento, las variables independientes o factores serán de tipo no métrico, y esto contempla dos posibilidades, ser de tipo nominal u ordinal. Esto conlleva diferencias conceptuales que debemos tener en cuenta.
Un factor es aleatorio, y por tanto de tipo nominal, si sus niveles consisten en una selección al azar de una población de niveles posibles. Un factor es considerado fijo, y por tanto de tipo ordinal, si sus niveles son escogidos premeditadamente por un procedimiento no aleatorio (Milliken y Johnson, 1992). Por ejemplo, en una muestra al azar de profesores en un estudio experimental sobre la influencia de distintos estilos de enseñanza en el rendimiento, la variable profesor constituiría un factor aleatorio. Si comparamos en cambio la eficacia de tres métodos didácticos concretos (A, B y C por ejemplo), éstos constituirían un factor de efectos fijos ya que se está específicamente interesado en estos métodos y no en otros. Se considera un modelo de efectos mixtos a aquél en el que uno o más factores son fijos y al menos uno es aleatorio.
En el caso del análisis de varianza de un factor, esta diferenciación no resulta imprescindible, ya que el cálculo de uno y otro modelo no supone diferencias más allá del nivel conceptual. No obstante debemos tener presente que son modelos diferentes.
En el modelo de efectos fijos se somete a prueba unos determinados niveles que son de nuestro interés, mientras que en el modelo de efectos aleatorios los factores son una muestra representativa de todos los posibles factores de un modelo de efectos fijos. Esta aparentemente diferencia superflua implica que en un modelo de efectos fijos la hipótesis nula sometida a prueba es que no hay diferencias con respecto a su media. Pero en el caso de efectos aleatorios se parte de que las medias serán iguales si la variabilidad de todas las medias es igual a cero, siendo esta la hipótesis nula que se pone a prueba.
Comparaciones múltiples.
El estadístico F, como se desprende del propio modelo inferencial de Neyman y Pearson, supone una respuesta de tipo dicotómico a la igualdad de las medias. Si la hipótesis nula es aceptada (es decir, las medias son iguales), hemos terminado, no hay mucho más que decir. Pero, si por el contrario encontramos diferencias estadísticamente significativas (es decir, rechazamos la hipótesis nula), nos queda resolver cual (o cuales) de los factores son los responsables del rechazo de la hipótesis nula.
Las posibles comparaciones que podemos realizar entre I factores será I – 1. Por tanto si tenemos como en nuestro problema de referencia 7 factores, tendremos 6 posibles comparaciones de medias independientes. Y la probabilidad de aceptar la igualdad de las 7 cuando realmente son iguales con un alpha de 0,05 será de:
(1 – 0,05)6 = 0,735
La probabilidad de rechazar al menos una cuando es verdadera será de:
1 – 0,735 = 0,265
Distinguiremos así dos tipos de comparaciones:
Comparaciones planificadas o a priori.- son las comparaciones que realizamos antes del análisis de los datos.
Comparaciones no planificadas o a posteriori o también post hoc.- son las comparaciones que nos permiten conocer cual es el factor responsable del rechazo de la hipótesis nula.
Las comparaciones que más importancia van a tener serán las comparaciones a posteriori, dado que estas nos descubren cual es el factor responsable del rechazo de la hipótesis nula, por tanto, no tienen sentido cuando la hipótesis nula es aceptada.
La prueba de Tukey.
El test HSD (honestly significant difference) desarrollado por Tukey realiza comparaciones entre medias (de dos en dos) pero fijando la tasa de error tipo I en alpha. Y esta es la prueba más usada.
Excel no tiene ninguna función predeterminada para hallar este valor, por lo que tendremos que recurrir a su formula para llevar a cabo el cálculo.
Tabla 3: Modelo de comparaciones múltiples de Tukey.

Para poder realizar los cálculos y obtener el valor HSD de Tukey necesitamos la tabla de rangos Studentizados, que puede descargar en pdf o en xls. Los cálculos son los siguientes:
El valor del rango Studentizado para:
Alpha = 0,05
Grados de libertad dentro de los niveles: 233
k - Número de factores o niveles en el análisis de varianza: 7
Por tanto el valor del rango Studentizado es de: 4,17 (dado que el valor máximo de la tabla equivale a 120).
Si nuestro modelo fuera equilibrado n tomaría el valor del tamaño de cada factor, pero como es diferente, tenemos que usar la media armónica del tamaño de los factores, que la designaremos por n’. Así n’ vale: 32,3077 (celda G69).
Con estos datos ya podemos calcular el valor HSD de Tukey, y toma el valor:
Formula 2: Diferencia máxima de Tukey.
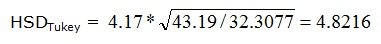
Por tanto, todas las diferencias de medias que en valor absoluto sean iguales o mayores que el valor 4.8216 serán responsables del rechazo de la hipótesis nula.
Tabla 4: Medias de los factores.
Así los factores C, D, E, F, y G no difieren en media entre si, ya que la diferencia entre ninguna de estas medias supera el valor 4,8216.
Los factores A y E difieren en su media ya que la diferencia en valor absoluto de sus medias es de 39,02 – 32,3 = 6,72.
De esta forma podemos saber que factores son responsables del rechazo de la hipótesis de igualdad de medias.
La prueba de Scheffé.
La prueba de Scheffé realiza comparaciones entre medias (de dos en dos) fijando la tasa de error tipo I en alpha. Esta prueba es más conservadora que la de Tukey, lo que nos llevara a considerar como iguales más medias de las que nos indicaba la prueba de Tukey.
Tabla 5: Modelo de comparaciones múltiples de Scheffé.

Por tanto:
n’ = 0,2167 (Celda I59)
Valor crítico de F = 2,1376
k = 7
MCerror = 43,19
Formula 3: Diferencia máxima de Scheffe.
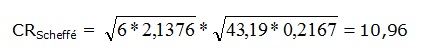
Como dijimos esta prueba es considerablemente más conservadora que la de Tukey, y dado que ninguna diferencia entre medias supera el valor 10,96, podemos concluir que todas son iguales. Una prueba es más conservadora cuanto más favorece la aceptación de la hipótesis nula.
Por último, y antes de entrar con SPSS, diremos que Excel tiene una opción, una vez instalada las herramientas de análisis, que permite la obtención del estadístico F para el ANOVA de un factor. Pero esta opción solo nos da el estadístico F, por lo que en el caso del rechazo de la hipótesis nula, no sabríamos que diferencias son las responsables del rechazo. La tabla que genera Excel puede verse en el rango J1:P20. Esta limitación nos lleva al análisis mediante SPSS.
Análisis de varianza de un factor con SPSS.
Como podemos ver con este análisis, los cálculos, si no complejos, ya se hacen muy laboriosos para realizarlos manualmente o con una calculadora, incluso con Excel, que aún facilitándolo muchísimo, hay que introducir muchas formulas. Por ello, cuando nos enfrentemos a las técnicas multivariantes, debemos recurrir a un programa de análisis estadístico avanzado, y SPSS cumple esta característica, además de disponer de grandes cantidades de documentación en Internet para la realización de los procedimientos e interpretación de las tablas de resultados.
El primer problema que nos vamos a encontrar cuando tratamos de realizar este análisis con SPSS es que, a diferencia de Excel, debe contener la variable dependiente en una columna, y los factores en otra. La disposición puede verse en el documento de referencia en la hoja SPSS. Además deberemos transformas el factor, nombrado en dicho documento con letras, en una numeración equivalente. Por ejemplo, si los factores eran A, B, C, D, E, F y G, ahora los llamaremos 1, 2, 3, 4, 5, 6, y 7 respectivamente, y asignarles como etiquetas el nombre de cada factor para que aparezcan referenciados en los términos que los hemos nombrado. Esto lógicamente tendrá repercusiones en la interpretación de las tablas, es decir, si transformamos A en 1, debemos tener esto en cuenta.
Para realizar un análisis de varianza de un factor pulsamos Analizar, comparar medias, y seguidamente ANOVA de un factor. Seleccionamos las comparaciones post hoc que deseamos, y tenemos cuidado con interpretar los resultados en función del supuesto de homogeneidad de varianzas. Si son iguales debemos considerar las diferencias de Tukey y Scheffe. Y si son diferentes, tendremos en cuenta las pruebas de T2 de Tamhane y T3 de Dunnett.
Una vez hecho esto, vamos a presentar algunas de las tablas que nos devuelve SPSS, el resultado completo del análisis se muestra en este documento.
Tabla 6: Estadísticos descriptivos.
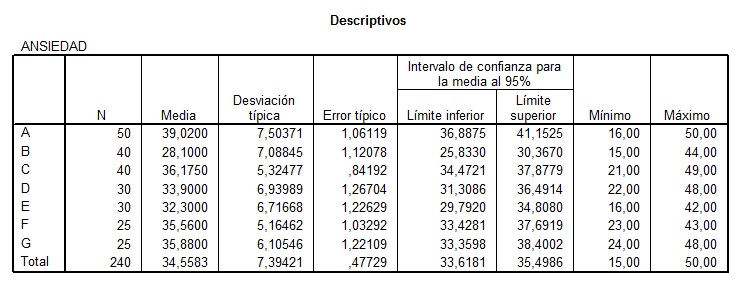
La tabla 6 nos muestra los principales estadísticos descriptivos y el intervalo de confianza con un alpha de 0,05 (1 - 0,95 = 0,05).
Tabla 7.

La tabla 7 nos muestra el estadístico de Levene para la homogeneidad de varianzas, dado que su valor de significación (0,223) es mayor que 0,05 (alpha), aceptamos que las varianzas son homogéneas o similares entre si. Recordemos que este supuesto es fundamental en el análisis de varianza, y nos indicara que diferencias post hoc debemos considerar para determinar la responsabilidad del rechazo de la hipótesis nula.
Tabla 8: Tabla resumen del ANOVA de un factor.
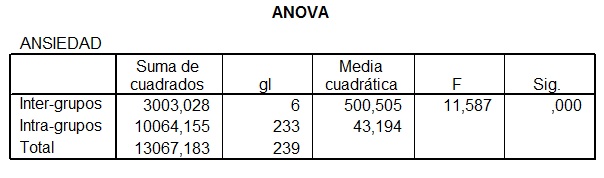
La tabla 8 nos ofrece los resultados que ya obtuvimos con Excel, y podemos ver como son idénticos, solo que en esta tabla no podemos ver el nivel crítico. La significación, dado que es menor que 0,05 nos permite rechazar la hipótesis nula que establece que las medias son iguales entre si.
Así, dado que son diferentes las medias, y dado que las varianzas son homogéneas, tendremos en cuenta las comparaciones post hoc de Tukey y Scheffé, las demás, no las tendremos en consideración. Estas tablas puede verla en la hoja de resultados de SPSS.
Tabla 9: Tabla de agrupación de factores según su igualdad de medias.
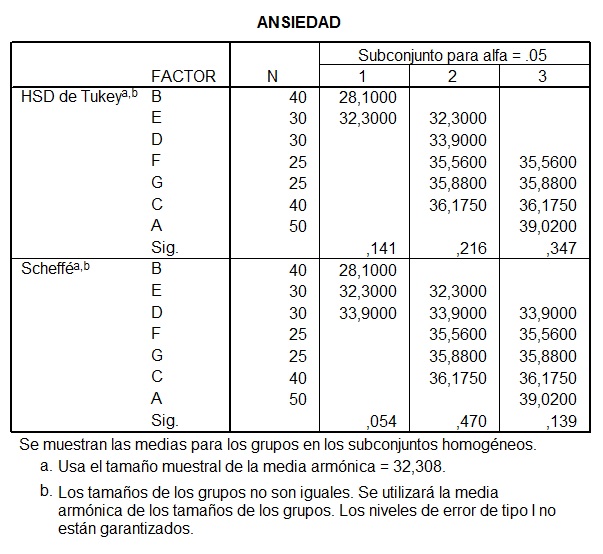
La tabla 9 nos muestra, en función de las correspondientes pruebas, que medias pueden ser consideradas similares, y con que grado de significación. Para la prueba de Tukey y Scheffé existen tres subconjuntos posibles según la similitud de sus medias. Así, los valores de significación mayores de 0,05 nos dicen que la media de esos factores es igual. Si atendemos al subconjunto 1 en la caso de Tukey, los factores B y E son iguales entre si, mientras que según Scheffé son iguales los factores B, E y D. Por supuesto, D y E en el caso de Tukey son diferentes, dado que pertenecen a subgrupos distintos, pero son iguales según Scheffé, dado que incluye como iguales esas diferencias en el mismo subconjunto. Recordemos que la prueba de Scheffé es más conservadora que Tukey.
Tabla 10: Gráfico de medias.
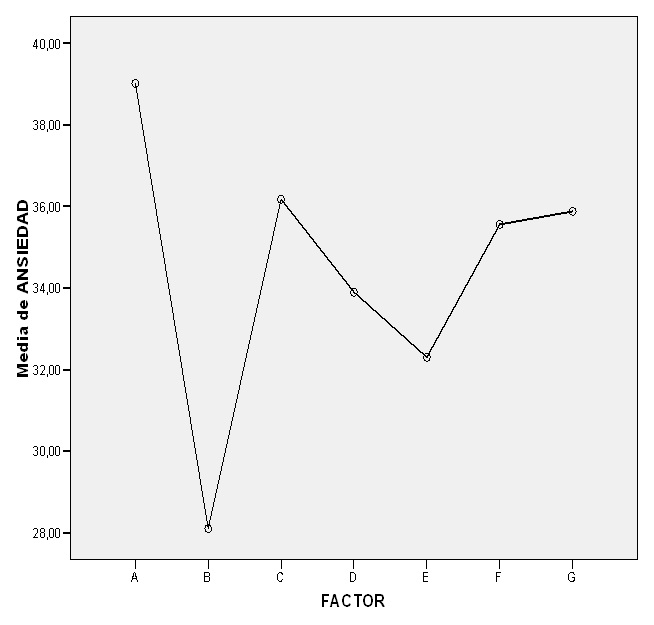
En la tabla 10 podemos ver la representación grafica de las medias que nos ofrece SPSS.
Con todo esto, ya podemos interpretar los resultados dentro del contexto de nuestra investigación.
Dado que:
Factor A: ambos sexos sin terapia de relajación.
Factor C: ambos sexos con la terapia tiempo B.
Factor F: hombres con terapia tiempo A.
Factor G: hombres con terapia tiempo B.
no difieren entre si, podemos afirmar que nuestra técnica de relajación como tratamiento reductor de la ansiedad, no parece tener un efecto reductor de la ansiedad.
No se encuentran diferencias entre los sujetos a los que se les aplica la terapia de relajación y los que no, no hay diferencias entre los sexos, y tampoco se ha podido constatar diferencias entre el tiempo de aplicación. Las diferencias entre factores parecen estar motivadas por el azar. Cabria, tras la observación del gráfico, decir que se aprecia una reducción en ansiedad en todos los casos de aplicación con respecto a cuando no hay terapia, y una acusada reducción de la ansiedad cuando ambos sexos han sido tratados simultáneamente con tiempo A. Sin embargo, esta tendencia no se ha mantenido en los demás casos. Cabria preguntarse si ha podido existir una variable extraña que pueda haber influido en los resultados.
Merece destacar que se rechazó la hipótesis nula de igualdad de medias, pero que las diferencias que se han producido, no lo han hecho en el sentido que se esperaba que lo hicieran, de ahí la importancia de plantear de manera adecuada las hipótesis de trabajo e interpretar los resultados basados en las hipótesis estadísticas, en función de la hipótesis de trabajo a la que queremos dar respuesta. Por tanto, no es solo que haya diferencias, sino que las diferencias se encuentren donde nuestra hipótesis de trabajo dice que sea importante que las haya.
Con todo esto, damos por finalizado los aspectos más básicos del análisis de varianza de un factor. Para quien este interesado en profundizar en el análisis con SPSS, visite este enlace.
Como reflexión final, y el lector ha podido constatar en este articulo, el software no resuelve el principal problema de la estadística, que técnica aplico, como la aplico, ni a que conclusiones llego. Solo resuelve el problema, que no es poco, de la realización de los cálculos matemáticos.
REFERENCIAS
COMENTARIOS
Publica tu comentario sobre este artículo
Anova en SPSS
Publicado por Maria. Fecha: 27-05-2015 07:49.
Anova en SPSS , tambien navegando encontre un curso completo on line donde te dan toda la información y también resuelven tus dudas. http://www.aqpvirtual.com/index.php/estadistica-en-spss
SOBRE LA PUBLICACIÓN
¿El artículo ha sido revisado? NO
Sobre el autor
- Nombre de usuario: ant123
- Formación: Máster
- Enviar mensaje al autor
- Fecha de publicación: 23-02-2012 13:43
- Actualice este artículo (Solo puede hacerlo su autor).
- Fecha de actualizacion: 23-02-2012 13:57